
블로그
-
발리가족여행_우붓맛집 와룽 장가르울람
와룽 장가르울람 warung Janggar ulam? 우붓맛집으로 유명한 장가르울람. 누사두아에서 우붓으로 이동, 아직 체크인 할 시간이 안됐길래 역시나 짐만 보관해두고 점심식사를 위해 리조트에서 나와서 바로 향했던 곳이다. ? ? 도로변... -
인도네시아 발리 ★ 와룽 장가르 울람
장가르 울람 문이 너무 너무 이쁘다 온통 파아란~ 파란 나라를 보았니?? 가 갑자기 생각남 ㅋㅋ 와룽 장가르 울람의 메뉴판 일단 메뉴 저렴하다 와룽 장가르 울람에서 보이는 우붓~ 곳곳이 눈이 맑게 해준다 나시고랭 립 사떼 와룽 -
울람바토르에 머물며...
울람바토르에 머무는동안 市內모습을 카메라에 담아보았다. 사회정서상 카메라 들이대는걸 무척 싫어하는 관계로,인물사진을 제외하고 조심스럽게 시내풍경을 담아보았다. 먼저 몽골은 한국에비해 해발고도가 무척높은곳에... -
발리 누사두아 맛집 - 인도네시아 현지식 울람(ULAM)
발리연수 2일차;) 오전에 풀빌라에서 쉬다가 바로 울람이라는 인도네시아 현지 식당으로 행했어요~ 인도네시아식이라기 보다는 발리식이래요! 울람은 고기라는 뜻이라고 하던데, 현지 맛집이라고 하더라구요~~~ 위치는 누사두아에... -
말레이시아 2013 - 말레이시아 샐러드 '울람' Ulam
소개를 하니 말 다 했죠. 향 초나 채 소가 쓴맛이 너무 많이 나지 만 않는다면 저는 안 가 리고 다 잘 먹는 편인데, '울람'에 쓰이는 우표 속 채 소 들 은 본 적도 먹어본 적도 없 어 몹 시 궁금합니다. 말레이어로 샐러드를 울... -
발리 누사두아맛집# 현지식레스토랑 울람(ULAM)
발리여행/ 발리 누사두아맛집 현지식레스토랑 울람 ULAM 짜잔 별이쒸에요. 어제는 하루 종일 리조트에서 딩굴거리며 놀아주셨던 별이쒸들 리조트식에 리조트내에서 맛사지도 받아주셨고 느므느므 행복이 퐁퐁 튀었지만 .... 비싸... -
누사두아 맛집-울람2(ULAM2)
리죠트 외부에서 식사하기가 마땅치 않은데 한국여행객들이 많이 찾는 현지식 식당이 울람2(ULAM2)식당 이다. 코트야드 메리어트 뒷쪽에 본점 울람(ULAM)이 있고 멜리아 브노아 리죠트 맞은편에 울람2(ULAM2)가 있다. 발리식... -
빌라스 발리 누사두아 - M갤러리 컬렉션, 울람...
먹으러 가기로 해요! 로비에서 로컬 푸드로 추천 받기도 했고, 다른 블로그 등등에서 자주 보기도 한 울람으로 가기로 합니다. 울람은 누사두아 리조트 쪽 내에 위치하고 있구요~ 아차차~ 누사두아 내에서 이동하는 거는~ 각... -
울람바트라에서 테렐지국립공원(Terelj National...
울람바타르를 출발해 테렐지공원을향해 달림니다. 울람바트라시내는 항상 차량정체가 대단하군요.흙먼지를비롯한 미세먼지와 자동차에서 나오는 배기가스까지.. 차선이 거의없고,좌핸들차량과 우핸들차량의 비율이 비슷하다보니... -
우붓맛집 JANGGAR ULAM장가르울람,인도네시아 음식
일단 배먼저 채우고 수영장을 가든지말던지 아아 수영장 Day 이젠 진짜 귀찮다!!!! Janggar ulam장가르 울람으로 궈궈 장가르 울람은 저희집에서 오토바이로 15분정도 걸립니다 가까운거리는아니져~ 겁나게 달리시다가 왼쪽에... -
외곽 라이스 뷰 레스토랑, 장가르 울람(Janggar Ulam)
<발리> Bali Ubub, 우붓 외곽 라이스 뷰 레스토랑, 장가르 울람(Janggar Ulam) ? 발리 우붓 체류기간: 2015년 1월 28일 ~ 2월 19일 (우붓 체류 중 렌트카 일주 진행) ? 우리의 숙소: Air B&B와 지인소개로 현지인 집을... -
짐바란씨푸드/누사두아울람/마해수아리/사왕안리조...
했다가 누워서 영화도 봤다가! 딱 우리가 생각했던 여행! 그리고 점심먹으러 가이드 주니님 만나러! ? 누사두아 "울람" 현지식 먹는 날이에요! 생선구이+각종야채 그냥 먹을만 했어요 ^^ 그냥 우린 다 잘 먹는걸로! 옆테이블에서... -
발리에서 생긴일에 나왔던 발리 현지 레스토랑 울람...
발리여행 왔으니 발리 현지식정도는 먹어주는 센스!! 우리가 가려는 울람 레스토랑은 노보텔 누사두아에서 차로 5분거리라 슬렁 슬렁 걸어서 산책와도 좋을만한 거리 였다 (발리 길거리는 생각보단 깔끔하더라구) 실제로 이렇게... -
발리여행 - 우붓 , 끄뜻리에르 , 장가르울람 -
배가 고프지요. 그래서 밥을 먹으러 갑니다. 이미 우붓외곽 에선 맛집으로 유명~한곳!! "장가르 울람" 입니다. 한국식으론 장갈울람?? 넓고 예쁜 푸른논과 연못이 함께 있는 우붓 특유의 풍요롭고 여유로와 보이는 인테리어~ 뭐... -
발리 맛집이라고? 누사두아 울람 맛집 평가 + 꾸따...
좋아~ 물놀이는 배고픔을 부르므로 자주 먹어줘야 한다 그리고 찾은 발리 누사두아 지역에서 꽤 유명한 레스토랑인 울람 좋다는 평이 많아 가보았는데 한마디로 완전 실망 개인 화로와 사태. 그나마 가장 나았으나 평평함 자체... -
맛집] 발리의 유명한 맛집들 (울람/누리스/부바검프)
[발리 맛집] 발리 현지식 맛집들 (울람/누리스/부바검프) #1. ULAM(울람) 울람은 1986년에 처음 문을 연 발리 전통 레스토랑으로 씨푸드 메뉴가 주를 이루고 있어요. 누사두아 지역에 위치해 있고, 지역내에서는 픽업&드롭서... -
발리맛집-울람
뒤편에 맛집이 많이 몰려있단걸 알아냄 후문에서 직진하면 바베큐 연기가 솔솔 나는곳으로 들어가면 된다 ㅎㅎ 울람-여기가 본점이라고함 일단 시원한 맥주부터 마시고 ㅎㅎ 나시고랭이 빠질수 없죠 ㅎㅎ 사떼 -생각보다 막... -
텔러-울람 설계, 수소폭탄의 원리
이글은 현재 사용되는 수소폭탄(열핵융합탄)의 기초가 되는 텔러-울람 설계를 파헤친 글입니다. 텔러-울람이 란? 텔러 울람은 핵탄두 디자인의 하나이다. 보통 "수소 폭탄 디자인"이라고 부르며, 미국에서 1951년, 소련에서 1953년에 -
우붓 맛집. 와룽 장가르 울람. warung janggar ulam
일단 점심 먹으러~! 책자에서도 보고, 별표 언니가 강추했던 와룽 장가르 울람 식당으로 고고씽했다. http://www.warungjanggarulam.com/ (와룽 장가르 울람 홈페이지) 우거진 숲 속으로 들어가니 짠!! 비밀의 화원인가!! 식당... -
[발리] 출발 (가루다항공) + 울람 (ULAM Balinese...
[발리] 출발 (가루다항공) + 울람 (ULAM Balinese Restaurant) 2014/08/12 ~ 2014/08/16 들뜬 마음을 안고 1년만에 또 비행기 탑승! 비행기 정말 많이 타본 나지만, 탈때마다 설레고 신난다. 그리고... 비행기 처음 타는 사람...

 에 대하여,
에 대하여, 이 존재한다. 여기서
이 존재한다. 여기서 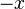 는
는  의
의 